教别人学习=自己补习
学习方法 | 01-07 10:39 12159次 13次
今天青果君想与你分享一种认知管理方法,也是一种学习方法:以教为学,通过教别人来学习。
用自然的语言,传递枯燥且有价值的知识,仿佛踩着高跷起舞,这并不容易。事实上,令人抓狂的数学题,也是可以用深入浅出的方式讲明白的。
诺贝尔奖物理学奖获得者,原子弹之父费费曼就是这方面的高手,费曼说,最好的学就是给别人讲。
所谓“费曼学习法”:通过向别人清楚地解说一件事,来确认自己真的弄懂了这件事。

不知你意识到没有,从古到今,全世界最牛的知识内容,都是以对话的形式存在的。
想想你脑海中的“子曰:学而时习之,不亦说乎”,就明白了。东方的孔子,西方的苏格拉底就是这方面的集大成者。
为什么说,教是最好的学?
教别人学习=自己补习
有时候,我们要讲一个概念,觉得很简单了,但在落笔的时候发现根本没办法把它用明确简单的话陈述出来——你说不清楚,实际上是因为你没理解这个概念。
①当你要去教别人的时候,会启动一种“保护效应机制”——你要保护自己的正确性,你要调动全部的知识和能力,让自己越过一个个逻辑漏洞。
②你教他的时候会想到一系列问题,比如“解这道题最简便的方法是什么?”,“如果概念解释不清楚,能不能用更简单的方法呢?”,这就需要你有一种打通知识和触类旁通的能力,或者说是一种知识融通的能力。
③“他会怎么理解这个概念”,“要想让他懂,关键点和结论是什么,如何论证,最难的是什么”。当你不断这样思考去辅导别人的时候,它会迫使你的表述尽可能地主动和具有创造性。
④在教别人过程中,通过别人的疑问、质疑、无视和新想法,会让我们对问题的认识更全面,有助于跳出固有思维模式。
⑤教别人学的过程其实是一种高强度的自学过程,你被迫去补各种各样的知识漏洞,横向、纵向扩展你的知识面,打通知识体系。
⑥根据艾宾浩斯遗忘曲线,教别人的过程,是一个强化重复记忆的过程,而且场景化知识更容易记住。

亚里士多德说,“哲学起源于好奇”,这个“好奇”一是兴趣,二是疑问:先有了问题才可能学习。换句话说就是:提取是最好的存储。
通过教别人,“提取”出一系列问题,接下来就是一个填坑的过程。所以,教别人与其说这是学习的过程,不如说是一个补习的过程。
以教为学的具体应用法门
第一步 - 选择一个你想要理解的概念,最好用思维导图的形式表现出来。
以绝对值为例 1.绝对值的几何定义: 一般地,数轴上表示数a的点与原点的距离叫做a的绝对值,记作|a|。 2.绝对值的代数定义: ⑴一个正数的绝对值是它本身; ⑵一个负数的绝对值是它的相反数; ⑶0的绝对值是0. 3.绝对值的性质 任何一个有理数的绝对值都是非负数,也就是说绝对值具有非负性。所以,a取任何有理数,都有|a|≥0。 4.绝对值的化简 ①当a≥0时, |a|=a ; ②当a≤0时, |a|=-a
第二步 - 设想一种场景,你正要向别人传授这个概念
物理大师和数学大师从O分别向东西方向步行10m,到达A,B两点,问:他们行走的距离是多少?路程相等吗? 这时,“绝对值”就发挥了它的作用:这种不考虑方向只研究大小的“符号的加工机”就叫做“绝对值”。 一般的,数轴上表示数a的点与原点的距离叫做a的绝对值,记作|a|。 绝对值即“距离”。 种距离就像姣爷和丹尼尔跨越11900公里相聚在伦敦查令十字街84号。
第三步 - 如果你感觉卡壳了, 就回顾一下学习资料
提出问题,如何巧用绝对值的非负性求值?如何运用数形结合思想和分类讨论思想化简绝对值问题?绝对值的易错点有哪些?
第四步 - 为了让你的讲解通俗易懂,简化语言表达
用你自己的语言,而不是学习资料中的语言来解释概念。再结合具体的试题讲解绝对值的简化、运算、思想等,知其然知其所以然,就是说要做的正确,讲得清楚,说的明白。
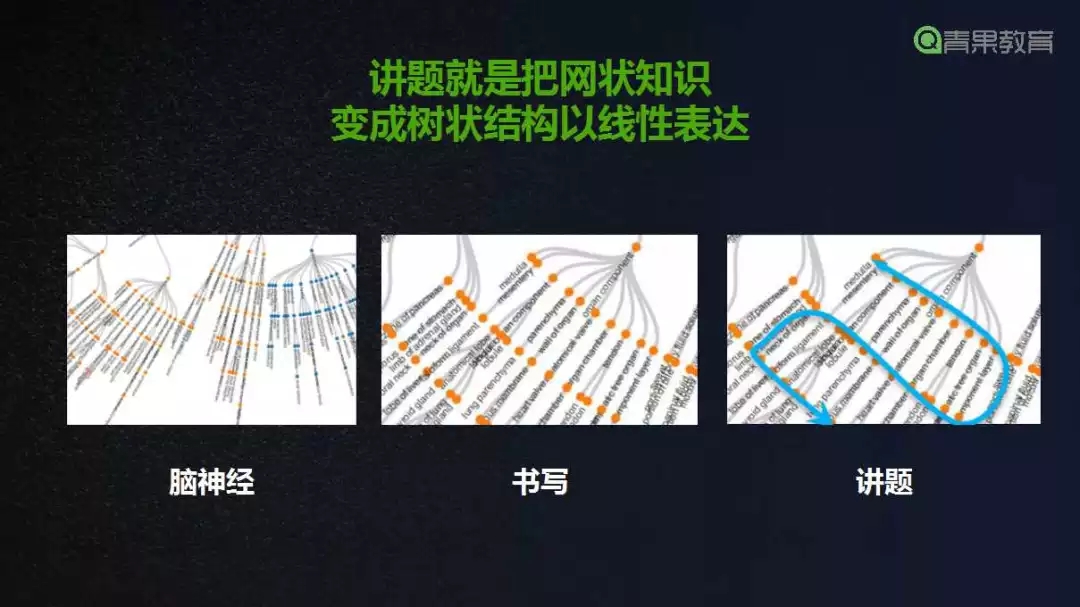
注:图片来自古典
当我们把所有的概念都弄清楚之后,用自己的话,把这个道题解法重新讲一遍, 只要别人能听懂你说的意思,那就说明你自己的学习成功了。
以教为学的过程中,会促使你更多的去思考,并且把基础知识做到了融会贯通。这也是一个刻意练习的过程。
文 青果教育整理发布,转载请注明出处
13人赞