数学发展史上出现过的三次危机的本质是什么？

这一节课，小编要讲讲数学，大家认真读。数学，算是所有科目中比较难学的一个科目，估计很多同学对数学是深恶痛绝！

你发现没有，对有些人却不一样（我们不一样，不一样！），他们一点都不觉得数学难学，反而觉得它很有趣。为了证明数学的有趣，小编给大家举个例子：

那么继续：

那接下来，有趣的事情发生了：

大家看到没？相等了。不是1≈0.999999…吗？怎么变成了相等？

关于1=0.999999……还是1≈0.999999……，这两个之间，到底是怎么回事？……好吧，小编也不能给出解释。

目前，对于这个问题，自然界有两个相反的说法，一个是0.999999循环，在自然界中，是根本不存在的，宇宙中没有任何一个实际物体，具有0.99...99这个数值……

另外一个猜测是：1的无穷次方等于1；而0.9999.....的无穷次方等于0，所以两者不相等……

很显然，这两个都是符合我们如今的数学认知，而且还相互矛盾的！这就更加让人难以明白，到底是等于，还是约等于，还是差距非常大！

这算是数学的一个悖论！但是！现在不明白，不等于以后不明白！数学，是一个发展的学科！

小编在这里，跟大家分享一下，数学的三次危机，都是因为数学发展过程中不够完善，差点断送了数学这个学科。

在公元前五世纪以前，数学学科毕达哥拉斯学派主张【“数”是万物的本原、始基】，而宇宙中一切现象都可归结为整数或整数之比，有理数理论成为占统治地位的数学规范……

毕达哥拉斯

小编这里先复习一下【有理数】的概念，它是整数（正整数、0、负整数）和分数的统称。这个有理数，是那个时候的数学的理论基石，不可动摇。

结果，在公元前580～568年间，一个毕达哥拉斯学派内部的一个成员希帕索斯，有一天突然发现：边长为1的正方形的对角线长度（根号2）既不是整数，也不能用整数之比来表示。

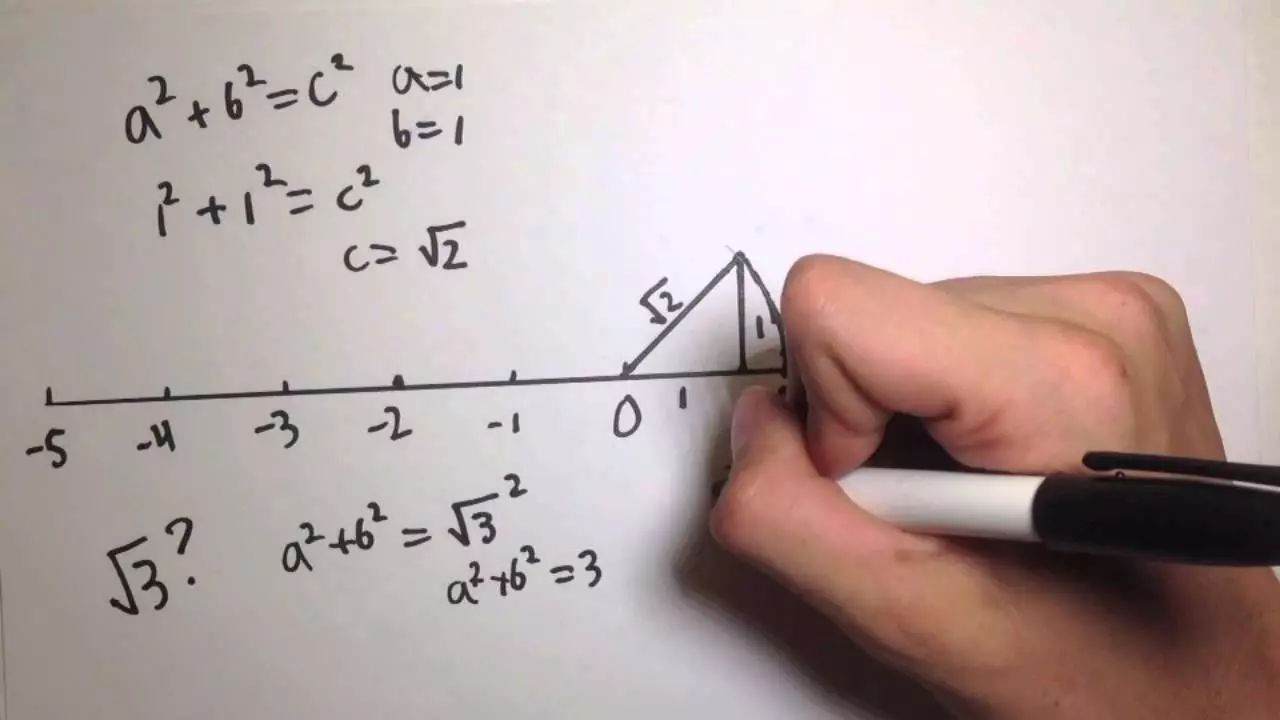
这一发现不仅严重触犯了毕达哥拉斯学派的信条，同时也冲击了当时希腊人的普遍见解，因此它直接导致了数学认识上的“危机”，动摇到了数学的根基。

这一悖论导致了Hipasus被毕达哥拉斯学派追杀，最终葬身大海的悲剧。

希帕索斯的这一发现，史称“希帕索斯悖论”，从而触发了第一次数学危机。

也正是因为这次数学悖论的出现，证明了人的直觉和经验不一定靠得住，而推理和证明才是可靠的，这就导致了亚里士多德的逻辑体系和欧几里德几何体系的建立……

过了两百年，希腊数学家欧多克斯和阿契塔斯两人给出了“两个数的比相等”的新定义，建立起一套完整的比例论，其中巧妙避开了无理数这一“逻辑上的丑闻”，并保留住与之相关的一些结论，缓解了这次数学危机。

然而，“世界万物皆为整数或整数比”的错误并没有解决，欧多克斯只是借助几何方法，直接避免无理数的出现。

直到1872年，德国数学家对无理数作出了严格的定义，无理数本质被彻底搞清，无理数在数学中合法地位的确立，才真正彻底、圆满地解决了第一次数学危机。

好了，这个第一次数学危机就讲到这里，回到1=0.999999……还是1≈0.999999……这个问题上来，就像这个根号2的出现动摇了当时的数学体系的情况一样，不相信根号2的存在……

而现在，有人不相信0.9999……无限循环不存在，不用担心，当未来数学发展到一定的程度时，它就存在了，也许到时候，会出现一个新的数学概念，1=0.999999……还是1≈0.999999这个问题，就像是当初的【无理数】概念一样……

17世纪末，牛顿和莱布尼茨分别独立地建立了微积分方法，成为解决众多问题的重要而有力的工具，并在实际应用中获得了巨大成功。

微积分是初等和高等数学的分水岭。莱布尼茨说：从人类有数学开始到牛顿时代，牛顿的贡献至少一半以上！尽管如此，从本质上说，还是科学技术的发展催生了微积分 。

17世纪，科学技术发展迅猛，向数学提出四类问题：瞬时速度问题；曲线的切线问题；函数极值问题；曲线长度和图形面积问题。以上四类问题吸引了大批数学家，产生了新的数学工具：坐标解析几何。

微积分的建立标志着数学从常数数学时代进入变数数学时代，推动了整个科学技术的发展。

然而，微积分学产生伊始，迎来的并非全是掌声，在当时它还遭到了许多人的强烈攻击和指责，原因在于当时的微积分主要建立在无穷小分析之上，而无穷小后来证明是包含逻辑矛盾的。

1734年爱尔兰主教贝克莱提出贝克莱悖论：无穷小量 dx 既是0又不是0！

无穷小量究竟是不是零？无穷小及其分析是否合理？这引起了数学界甚至哲学界长达一个半世纪的争论。

如果解不到这个问题，所谓无坚不摧的微积分，便无立足之地，一切由微积分所得出来的完美的数学和物理学上的结果也付诸流水，所以数学史上称之为“第二次数学危机”。

 数学是讲究严谨的学科，数学家必不逃避问题，面对困难，接受挑战，是数学家的不朽格言。

化解这一悖论的重大科学发现是极限论，它使得微积分得以严密化。

1820年，另一位伟大的数学家柯西（1789–1857），重新建立微积分学的基础——数学分析。

数学分析是透过一套严格的“数学语言——ε–语言”来说明甚么是变量、无穷小和极限等的概念和定义，解决了甚么是既不是零又不是非零的问题，而这次的危机亦安然渡过，并为数学的大家庭增添了一位成员“数学分析”。

魏尔斯托拉斯进一步改进柯西的工作，给出极限的 e--d 语言定义：

经过数位杰出数学家对于微积分学基础概念的重建后，第三次数学危机才终于得以解决。

19世纪后期，高等数学（微积分），线性代数（多项式，矩阵，行列式），几何学（射影几何）已经发展得十分完备； 

一些新的数学分支，如泛函分析，抽象代数，拓扑学，等等，开始出现；

康托建立了集合论-----现代数学的基础。

1900年庞加莱称：数学的严格性，看来直到今天才可以说是实现了。正在此时，罗素定义的集合R：所有不以自己为元素的集合所组成的集合R = { x | x ? x } 。

这个漏洞就源于英国数学家罗素提出的一个悖论：所有不包含自身的集合的集合，它到底包不包含自身呢？如果它包含自身，那么它就不是不包含自身的集合，所以也就不是所有不包含自身的集合的集合的元素。

伯特兰·罗素(Bertrand Russell，1872.5.18-1970.2.2)

如果它不包含自身，那它理应是所有不包含自身的集合的集合的一个元素。这样的一个集合，包不包含自身，都必将引发矛盾。

对于罗素悖论，有一个通俗的故事可以解释，就是“理发师悖论”。

罗素悖论一经提出便在当时的数学界与逻辑学界内引起了轩然大波，直接导致了第三次数学危机！

弗雷格（Friedrich Ludwig Gottlob Frege，1848.11.8-1925.7.26)

由于这个悖论，费雷格的著作《算术原理》中的第五公理竟然是错的！他感觉算术的基础发生了动摇。

最后只能在自己著作的末尾写道：“一个科学家所碰到的最倒霉的事，莫过于是在他的工作即将完成时却发现所干的工作的基础崩溃了。”

那么，这次危机是如何得到解决的呢？

事实上，为了解决罗素悖论，演化出逻辑主义，直觉主义，形式主义等数学学派，产生了集合论的公理化。人们注意到，必须对康托的朴素集合论加以限制，限制到足以排除悖论，同时保留所有有价值的东西。 

庞加莱说，我们建造了一个围栏来放养羊群，以防止它们被狼侵害，但我们不知道在围栏中是否已经有狼。

直到1931年，哥德尔提出了一系列不完备定理并予以证明：

至此，这场关于数学基础的争论终于结束，同时也宣告了把数学彻底形式化的愿望是不可能实现的。

数学是讲究严谨的学科，数学家必不逃避问题，面对困难，接受挑战，是数学家的不朽格言。

历史上的三次数学危机，虽然给人们带来了极大的麻烦，但是危机的产生使人们认识到了现有理论的缺陷，并不断去完善，由此，数学也会得到新的发展，甚至会有革命性的的变革！

事实上，悖论的产生往往预示着科学的发展，可以说，悖论是科学发展的产物，是科学发展源泉之一。

第一次数学危机使人们发现无理数，建立了完整的实数理论，欧氏几何也应运而生并建立了几何公理体系；

第二次数学危机的出现，直接导致了极限理论、实数理论和集合论三大理论的产生和完善，使微积分建立在稳固且完美的基础之上；

第三次数学危机,使集合论成为一个完整的集合论公理体系（ZFC系统）,促进了数学基础研究及数理逻辑的现代性。